FX
Talk Of The Trade: What's A Risk Reversal ?
Risk reversals are a useful real-time gauge of speculative interest in currencies
Published ET
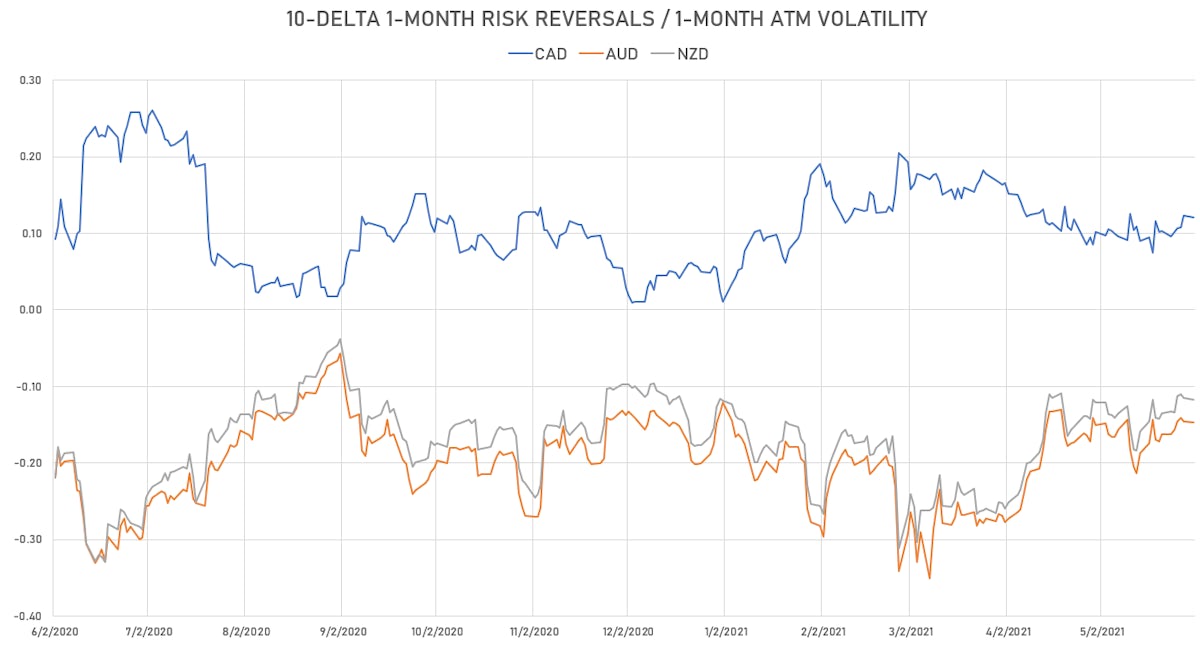
1-Month 10-Delta Risk Reversals for the CAD, AUD, NZD | Sources: ϕpost, Refinitiv data
We will from time to time define concepts, which we think should be understood by all our readers. So here we go: what is a risk reversal and why does it matter ?
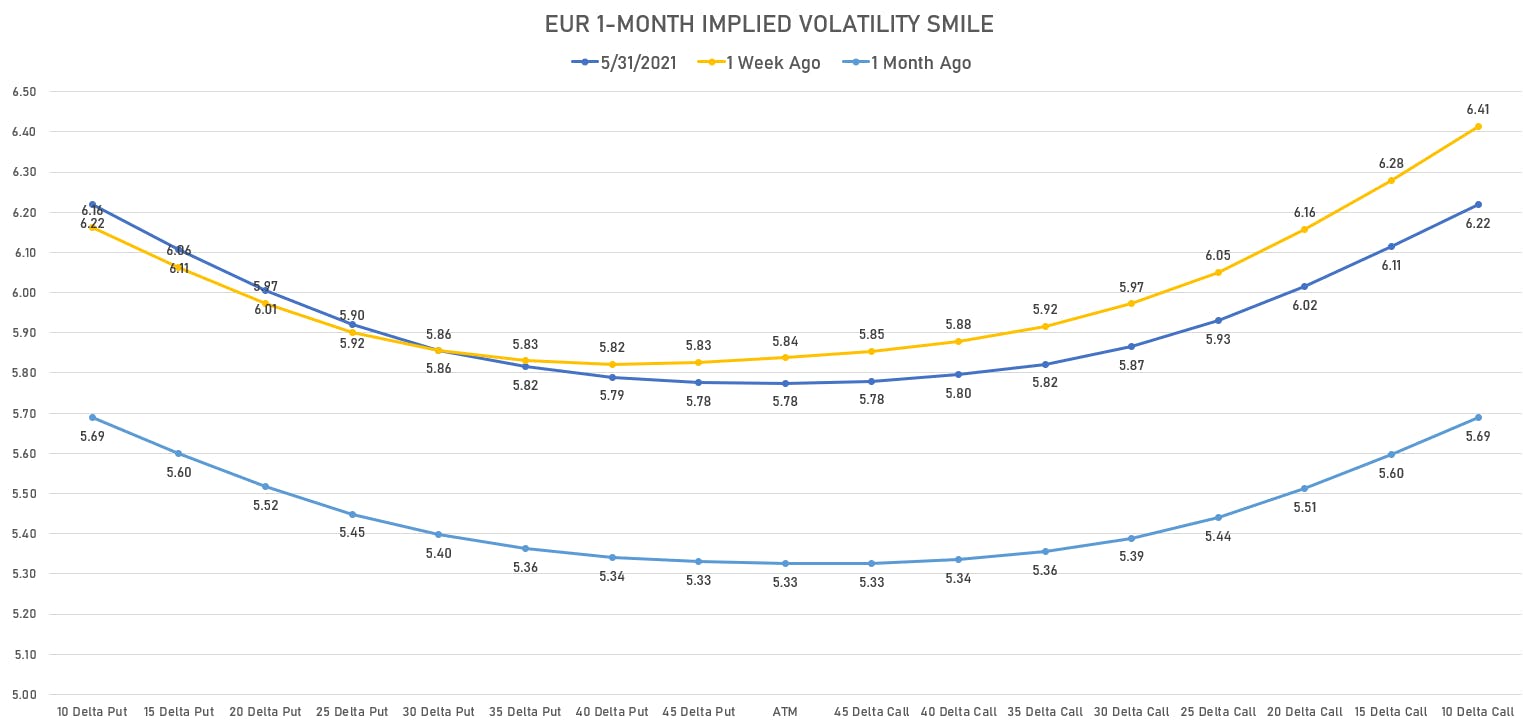
IMPLIED VOLATILITY SMILE
Let's take a few steps back before jumping in:
- Currency options markets give information about speculative interest on either side of the current spot price (up or down).
- The price of an option is sensitive to a change in the spot price of the currency: this sensitivity is called delta (how much the price of an option changes when the price of the currency changes).
- The delta is smaller as the strike price of the option is further away from the current spot price: for example, if the euro spot price is 1.2200, an option with a strike price of 1.2400 has a higher delta than an option with a strike price of 1.2650
- The delta of an ATM (at-the-money) option is 0.50, and the delta of out-of-money options is smaller than that. The delta is usually quoted like a percentage: for instance an option with a delta of 0.35 will be called a 35-delta.
- For a given level of delta and a given maturity, the price of a regular "vanilla" option can be largely reduced to the implied volatility of the option
- So you can build a curve, called the "volatility smile" (see below), which presents the implied volatility (IV for short) of options at different levels of delta. Usually, the price of an option (its IV) is higher as the strike price is further away from the spot (meaning the curve slopes higher on either side of the spot price).
WHY IS THAT IMPORTANT
- The volatility smile provides a visual comparison of how expensive options are for a given level of delta on the upside and downside.
- So you can very quickly see whether the upside and downside are priced equally, or whether one side is more expensive.
- When the curve is skewed to one side, it gives a direct indication of what options market see as more likely to happen. Or said differently: it shows which expectation is already priced in by the market. For example: if the 10-delta put has an IV of 5.80 and the 10-delta call an IV of 6.30, the market has already bet that the spot price is likely to rise.
RISK REVERSAL
- The difference between the price of a call and a put with the same expiry and the same delta is called a risk reversal (RR for short)
- For example: a 40-delta RR = 40-delta call - 40-delta put
- It can be used as an option strategy: if you own the underlying currency, you can build a hedge by selling a risk reversal (i.e. buy an out-of-the-money put by selling an out-of-the-money call). You just give up some upside in order to get downside protection.
- Perhaps more importantly: looking at the prices of RRs gives you a sense of what options markets have already priced in for the underlying currency.
- Illustration: if a 10-delta RR is very expensive, it means that speculators are already disproportionately on one side of the trade (the upside). Does that mean the currency will not go up and is about to revert? Not necessarily. Speculators are often positioned on the correct side of the trade: in this case, it would mean that the currency has a good chance to rise. But it also means that the time to buy might have passed as many market participants are already in the trade. In other words: watch for the moves in the RR rather than the levels.
- Following RRs in a price chart gives real-time information on the ebbs and flows of speculative interest.
- Note that we will often present the RR IV divided by the ATM IV (see chart below), in order to make it comparable historically and because we're not interested in RR moves driven by moves in the ATM.
